Designing a k-NN Algorithm

k-NN Algorithms with Multiple Nearest Neighbors Considered

In the previous classifier example, you only considered the closest neighbor when designing the algorithm to deduce the unknown fish's label. In reality, this can be risky as any outlier can severely influence our decisive power. Imagine if, instead, the unknown fish's width was 1.5 and the length was 1.5. The unknown fish would then be plotted at the following location:

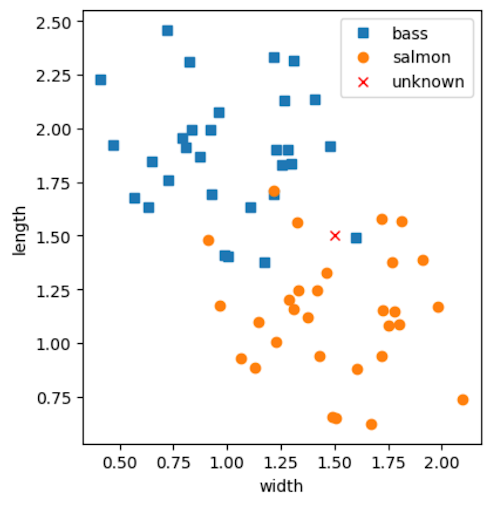
Your intuition may still tell you that the unknown fish is likely a salmon, as it is in the graph's heavily "salmon-populated" region. However, the one bass outlier closest to the unknown fish is, in fact, the most similar fish (as decided by our algorithm) to the unknown fish, and this would result in the unknown fish being classified as a bass.

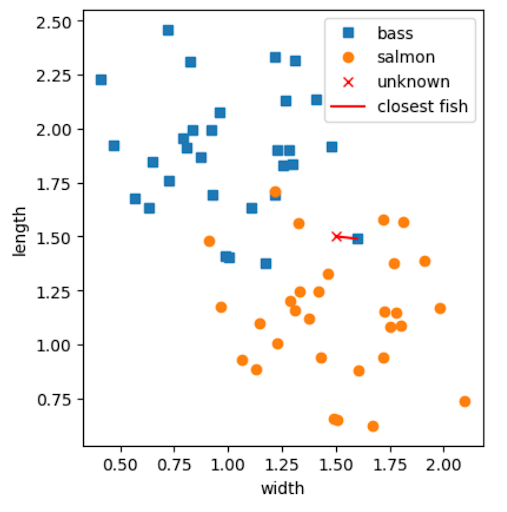
This is problematic! Though our classifier is fully functional to our specifications, and though it will be accurate a majority of the time, it will not always predict what our intuition tells us what it should predict.

An idea: what if you designed the classifier to take into account the $k$ closest neighbors to the unknown fish? Then, you can assign the unknown fish's label to be the most common fish label out of the $k$ nearest neighbors.

This algorithm is called k-Nearest Neighbors (k-NN), and is often preferred over NN (also called 1-NN as $k=1$)!

Let's alter our algorithm to consider the k nearest neighbors.

1. Calculate the distance between the unknown fish and every fish in the training dataset
2. Find the shortest $k$ distances for all calculated distances
3. Find each fish that corresponds to each $k$ shortest distances
4. Find each label that corresponds to these specific $k$ fish
5. Set our unknown fish's label to the most popular label of these $k$ fish

For instance, let's examine the case where $k=3$ for our fish classification problem. If we apply this new algorithm to our data we obtain the following results:

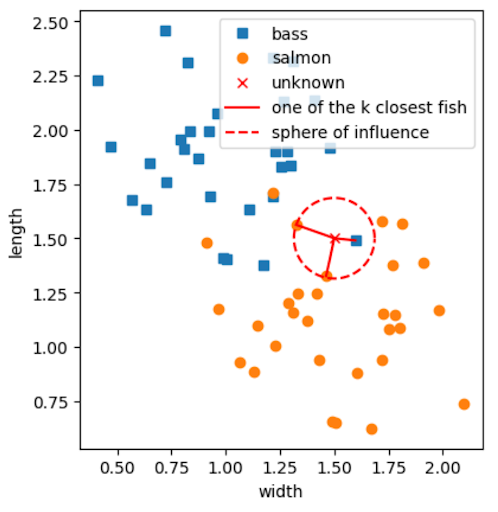
The majority of the neighboring fish are indeed salmon! Therefore, we can label the unknown fish as a salmon for the $k=3$ case of k-NN.

As a result of choosing more nearest neighbors (a higher $k$ value) for the decision mechanism, we were able to mitigate the effect of noise (i.e. outliers) on our classification system.